Examples

Here we show a selection of examples of using cweqgen.

Generating an equation

To generate an equation you just need the correct name for the equation, as given in the Equations section, and the equations() function. To generate the equation for the gravitational-wave amplitude \(h_0\) you would do:

from cweqgen import equations
eq = equations("h0")

If you print the returned EquationBase object (called eq in this case) it will return a LaTeX string, via the equation() method, giving the equation (note that the equation is not enclosed in “$” symbols):

print(eq)

% equation generated with cweqgen v0.4.2.dev2+gb08a31c.d20220426:
%   equations(equation="h0")
h_0 = \frac{16 G}{c^{4}} \pi^{2}\frac{\varepsilon I_{zz}}{d} f_{\rm rot}^{2}

If working in a Jupyter notebook, you can show the typeset LaTeX equation by just running a cell containing eq:

eq

$% equation generated with cweqgen v0.4.2.dev2+gb08a31c.d20220426: % equations(equation="h0") h_0 = \frac{16 G}{c^{4}} \pi^{2}\frac{\varepsilon I_{zz}}{d} f_{\rm rot}^{2}$

Equation as a figure

You can return an equation as an object containing a matplotlib.figure.Figure, which can then be saved in whatever format you require by using the equation() method with the displaytype keyword set to "matplotlib". If running this in a Jupyter notebook, a png version of the equation will be shown.

fig = eq.equation(displaytype="matplotlib")
fig.savefig("myequation.pdf")  # save a pdf version of the equation

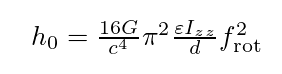
Equation with fiducial values

Each equation is defined with a set of “fiducial” values. A LaTeX string containing a version of the equation evaluated at the fiducial values can be created using the fiducial_equation() method:

print(eq.fiducial_equation())

% equation generated with cweqgen v0.4.2.dev2+gb08a31c.d20220426:
%   equations(equation="h0")
h_0 = 4.23 \times 10^{-26} \; \mathrm{}\left(\frac{I_{zz}}{1 \times 10^{38} \; \mathrm{m^{2}\,kg}}\right) \left(\frac{\varepsilon}{1 \times 10^{-6} \; \mathrm{}}\right) \left(\frac{1 \; \mathrm{kpc}}{d}\right) \left(\frac{f_{\rm rot}}{100 \; \mathrm{Hz}}\right)^{2}

If running this in a Jupyter notebook, it can display the typeset LaTeX equation:

eq.fiducial_equation()

$h_0 = 4.23 \times 10^{-26} \; \mathrm{}\left(\frac{I_{zz}}{1 \times 10^{38} \; \mathrm{m^{2}\,kg}}\right) \left(\frac{\varepsilon}{1 \times 10^{-6} \; \mathrm{}}\right) \left(\frac{1 \; \mathrm{kpc}}{d}\right) \left(\frac{f_{\rm rot}}{100 \; \mathrm{Hz}}\right)^{2} $

The fiducial_equation() method can also take the displaytype="matplotlib" keyword argument to return a Matplotlib Figure containing the equation.

Setting fiducial values

You can generate the equation with different fiducial values. You can either do this when creating the EquationBase object by passing equations() your own values, e.g.:

eq = equations("h0", ellipticity=1e-7, distance=2.5)
eq.fiducial_equation()

$h_0 = 1.69 \times 10^{-27} \; \mathrm{}\left(\frac{I_{zz}}{1 \times 10^{38} \; \mathrm{m^{2}\,kg}}\right) \left(\frac{\varepsilon}{1 \times 10^{-7} \; \mathrm{}}\right) \left(\frac{2.5 \; \mathrm{kpc}}{d}\right) \left(\frac{f_{\rm rot}}{100 \; \mathrm{Hz}}\right)^{2} $

or do it through fiducial_equation():

eq.fiducial_equation(momentofinertia=2e38, rotationfrequency=200)

$h_0 = 1.35 \times 10^{-26} \; \mathrm{}\left(\frac{I_{zz}}{2 \times 10^{38} \; \mathrm{m^{2}\,kg}}\right) \left(\frac{\varepsilon}{1 \times 10^{-7} \; \mathrm{}}\right) \left(\frac{2.5 \; \mathrm{kpc}}{d}\right) \left(\frac{f_{\rm rot}}{200 \; \mathrm{Hz}}\right)^{2} $

If you pass fiducial values as dimensionless values the default units from the equation definitons will be assumed. However, you can pass values with astropy Unit types and these will get correctly intepreted. For example, if you wanted to have the fiducial distance of 1000 light years and the principal moment of inertia in cgs units, you could use:

from astropy.units import Unit
eq = equations("h0", distance=1000 * Unit("lyr"), momentofinertia=1e45 * Unit("g cm^2"))
eq.fiducial_equation()

$h_0 = 1.38 \times 10^{-25} \; \mathrm{}\left(\frac{I_{zz}}{1 \times 10^{45} \; \mathrm{cm^{2}\,g}}\right) \left(\frac{\varepsilon}{1 \times 10^{-6} \; \mathrm{}}\right) \left(\frac{1 \times 10^{3} \; \mathrm{lyr}}{d}\right) \left(\frac{f_{\rm rot}}{100 \; \mathrm{Hz}}\right)^{2} $

The keywords for providing the fiducial values can be from a range of aliases given in cweqgen.definitions.ALLOWED_VARIABLES.

Evaluating the equation

The EquationBase class does not only provide ways to output LaTeX strings, but can also be used to evaluate the equation at given values. To can be done using the evaluate() method. If no values are provided to evaluate() it will return the equation as evaluated at the default fiducial values (or those provided when initialising the equation), e.g.:

eq = equations("h0")
eq.evaluate()

$4.2285561 \times 10^{-26} \; \mathrm{}$

The EquationBase actually has a __call__ method defined allowing you to use EquationBase objects as functions by running the evaluate() method, e.g.,

eq()

$4.2285561 \times 10^{-26} \; \mathrm{}$

You can pass values for any of the variables in the equation to calculate it at those values (any variable not provided will still assume the fiducial values). Values can have astropy Unit types, but if not the default units will be assumed. You can also pass arrays of values, e.g.:

eq.evaluate(distance=[1.0, 2.0, 3.0] * Unit("kpc"))

$[4.2285561 \times 10^{-26},~2.114278 \times 10^{-26},~1.4095187 \times 10^{-26}] \; \mathrm{}$

If you pass equal length arrays then the output will be the same length as the inputs (i.e., the equation is evaluate by each index in the arrays):

eq.evaluate(distance=[1.0, 2.0, 3.0] * Unit("kpc"), rotationfrequency=[50, 100, 150] * Unit("Hz"))

$[1.057139 \times 10^{-26},~2.114278 \times 10^{-26},~3.1714171 \times 10^{-26}] \; \mathrm{}$

However, if you require values on a mesh grid of values, you can add the mesh=True keyword argument:

eq.evaluate(distance=[1.0, 2.0, 3.0] * Unit("kpc"), rotationfrequency=[50, 100, 150] * Unit("Hz"), mesh=True)

$[[1.057139 \times 10^{-26},~5.2856951 \times 10^{-27},~3.5237967 \times 10^{-27}],~ [4.2285561 \times 10^{-26},~2.114278 \times 10^{-26},~1.4095187 \times 10^{-26}],~ [9.5142512 \times 10^{-26},~4.7571256 \times 10^{-26},~3.1714171 \times 10^{-26}]] \; \mathrm{}$

If arrays of different lengths are passed to evaluate() then it will automatically perform the evaluation on a mesh grid.

eq.evaluate(ellipticity=[1e-6, 1e-7], rotationfrequency=[50, 100, 150] * Unit("Hz"), mesh=True)

$[[1.057139 \times 10^{-26},~1.057139 \times 10^{-27}],~ [4.2285561 \times 10^{-26},~4.2285561 \times 10^{-27}],~ [9.5142512 \times 10^{-26},~9.5142512 \times 10^{-27}]] \; \mathrm{}$

Rearranging an equation

You can rearrange an equation to switch the value on the left hand side with one of the other variables. This uses the rearrange() method, which returns a new EquationBase (the original EquationBase will not be changed):

# equation for the braking index
eq = equations("brakingindex")

# rearrange to put frequency derivative on the lhs
req = eq.rearrange("rotationfdot")
req.equation()

$\dot{f}_{\rm rot} = \frac{1}{n^{1/2}} \left(\ddot{f}_{\rm rot} f_{\rm rot}\right)^{1/2}$

The fiducial values for the old right hand side variable will be set from the value evaluated at the fiducial values from the original equation. However, a new fiducial value can be set by passing it to rearrange(), e.g.:

# set fiducial value for the braking index of 4!
req = eq.rearrange("rotationfdot", 4)
req.fiducial_equation()

$\dot{f}_{\rm rot} = 1.12 \times 10^{-11} \; \mathrm{\frac{Hz}{s}}\left(\frac{4 \; \mathrm{}}{n}\right)^{1/2} \left(\frac{\ddot{f}_{\rm rot}}{1 \times 10^{-23} \; \mathrm{\frac{Hz}{s^{2}}}}\right)^{1/2} \left(\frac{f_{\rm rot}}{50 \; \mathrm{Hz}}\right)^{1/2} $

Substituting an equation

It is possible to substitute one equation into another using the substitute() method. If we take the above rearranged equation giving rotation frequency derivative in terms of braking index, rotation frequency and frequency second derivative, it can be substituted into the equation for the gravitational-wave amplitude spin-down limit:

from cweqgen import equations

# equation for the braking index
eq = equations("brakingindex")

# rearrange to put frequency derivative on the lhs
req = eq.rearrange("rotationfdot")

eqsd = equations("h0spindown")
subeq = eqsd.substitute(req)  # substitute in req
subeq.equation()

$h_0^{\rm sd} = \frac{\sqrt{10} \sqrt{G}}{2 c^{3/2}}\frac{I_{zz}^{1/2} \left|{\ddot{f}_{\rm rot}}\right|^{1/4}}{d f_{\rm rot}^{1/4} \left|{n}\right|^{1/4}}$

Another useful example is getting the gravitational-wave amplitude in terms of the mass quadrupole \(Q_{22}\). This can be achieved with:

# equation for gravitational-wave amplitude
eqh0 = equations("h0")

# equation for mass quadrupole (in terms of ellipticity and moment of inertia)
eqq22 = equations("massquadrupole")

# rearrange and substitute
eqh0q22 = eqh0.substitute(eqq22.rearrange("ellipticity"))
eqh0q22.equation()

$h_0 = \frac{32 \sqrt{30} \pi^{5/2} G}{15 c^{4}}\frac{Q_{22}}{d} f_{\rm rot}^{2}$

Equivalent variables

Some equations allow you to pass in variables that are equivalent (bar some conversion) to the required variables, e.g., using rotation period when rotation frequency is required:

eq = equations("ellipticityspindown")
eq.equation()

$\varepsilon^{\rm sd} = \frac{\sqrt{10} c^{5/2}}{32 \pi^{2} \sqrt{G}}\frac{\left|{\dot{f}_{\rm rot}}\right|^{1/2}}{I_{zz}^{1/2} f_{\rm rot}^{5/2}}$

# evaluate using rotation period rather than rotation frequency
eq.evaluate(rotationperiod=0.05 * Unit("s"))

$0.00033715079 \; \mathrm{}$

Converting between frequencies

If an equation contains a frequency parameter (or equivalently a rotation period) and/or its first derivative you can convert it to another frequency parameter using the to() method. For example, an equation containing rotation frequency can be converted to one with rotation period:

eq = equations("h0spindown")

neweq = eq.to("rotationperiod")
neweq.eqn

$h_0^{\rm sd} = \frac{\sqrt{10} \sqrt{G}}{2 c^{3/2}}\frac{I_{zz}^{1/2} \left|{\dot{P}}\right|^{1/2}}{d P^{1/2}}$